
The goal of the formula is to determine the optimal amount to put into any one trade. There are two key components to the formula for the Kelly criterion:. The result of the formula will tell investors what percentage of their total capital they should apply to each investment.
The term is often also called the Kelly strategy, Kelly formula, or Kelly bet, and the formula is as follows:. While the Kelly Criterion is useful for some investors, it is important to consider the interests of diversification as well.
Many investors would be wary about putting their savings into a single asset—even if the formula suggests a high probability of success. The Kelly Criterion formula is not without its share of skeptics.
Although the strategy's promise of outperforming all others, in the long run, looks compelling, some economists have argued against it—primarily because an individual's specific investing constraints may override the desire for optimal growth rate.
In reality, an investor's constraints, whether self-imposed or not, are a significant factor in decision-making capability. The conventional alternative includes Expected Utility Theory, which asserts that bets should be sized to maximize the expected utility of outcomes.
The Kelly Criterion is a formula used to determine the optimal size of a bet when the expected returns are known. According to the formula, the optimal bet is determined by the formula. It was first adopted by gamblers to determine how much to bet on horse races, and later adapted by some investors.
Unlike gambling, there is no truly objective way to calculate the probability that an investment will have a positive return. Most investors using the Kelly Criterion try to estimate this value based on their historical trades: simply check a spreadsheet of your last 50 or 60 trades available through your broker and count how many of them had positive returns.
In order to enter odds into the Kelly Criterion, one first needs to determine W, the probability of a favorable return, and R, the size of the average win divided by the size of the average loss.
For investing purposes, the easiest way to estimate these percentages is from the investor's recent investment returns. These figures are then entered into the formula. While there are many investors who integrate the Kelly Criterion into successful moneymaking strategies, it is not foolproof and can lead to unexpected losses.
Many investors have specific investment goals, such as saving for retirement, that are not well-served by seeking optimal returns. Some economists have argued that these constraints make the formula less suitable for many investors. The Black-Scholes Model, Kelly Criterion, and the Kalman Filter are all mathematical systems that can be used to estimate investment returns when some key variables depend on unknown probabilities.
The Black-Scholes model is used to calculate the theoretical value of options contracts, based upon their time to maturity and other factors.
The Kelly Criterion is used to determine the optimal size of an investment, based on the probability and expected size of a win or loss. The Kalman Filter is used to estimate the value of unknown variables in a dynamic state, where statistical noise and uncertainties make precise measurements impossible.
While some believers in the Kelly Criterion will use the formula as described, there are also drawbacks to placing a very large portion of one's portfolio in a single asset. You may accept or manage your choices by clicking below, including your right to object where legitimate interest is used, or at any time in the privacy policy page.
These choices will be signaled to our partners and will not affect browsing data. Accept All Reject All Show Purposes. Fundamental Analysis Tools. Trending Videos. What Is Kelly Criterion? Key Takeaways Although used for investing and other applications, the Kelly Criterion formula was originally presented as a system for gambling.
The Kelly Criterion was formally derived by John Kelly Jr. The formula is used to determine the optimal amount of money to put into a single trade or bet. Several famous investors, including Warren Buffett and Bill Gross, are said to have used the formula for their own investment strategies.
Some argue that an individual investor's constraints can affect the formula's usefulness. What Is the Kelly Criterion? Who Created the Kelly Criteria?
But who would build that? Here is the rate example. Just press calculate and the calculator does the rest for us. It even lets us figure out where given percentiles will fall after a given number of bets. You can do that either using the normal approximation or by running a Monte Carlo simulation.
Here is a list of what it gives and what they mean: E log X : This is the average of what a bet does to the log of your net worth. Average Rate of Return: If you follow the betting strategy for a long time, your final return should be close to earning this rate per bet. With compounding returns.
Volatility: The standard deviation of what happens to the log of your net worth. This number drives how much your real returns will bounce above or below the long term average in the short run.
This is a measure of risk. If your average rate of return is positive and this is below 5, you're unlikely to be losing money after 50 bets. If this is below 7 then you're unlikely to be losing money after bets. If this is a lot higher than that, you'd better be ready for a financial roller-coaster.
Percentile X, n bets - rate of return: After n bets, if your result is at percentile X, what effective interest rate did you get per bet compounding? This can be estimated through the normal approximation or a Monte Carlo simulation.
Percentile X, n bets - final result: After n bets if your result is at percentile X, how much was your money multiplied by? The normal simulation may give somewhat unrealistic answers. Now there is actually a second calculator that only can handle 1 bet. It is like the first but has the nice feature that you can automatically optimize allocations.
That means that it figures out the right amount to bet for maximum returns before doing anything else. You can choose whether to maximize your long-term returns, or to optimize where you'd be if after a fixed number of bets you were at a particular scenario. As the note on the calculator says, it estimates returns using a normal approximation and then optimizes that.
So the answers you get are good, but not perfect. What is the optimal fraction of our bankroll to bet? That rule is simple and memorable, but what happens when the bet gets more complex? What is the optimal portion of your net worth to bet?
Well most gamblers would say, "edge over odds". But what are your odds? Do you weight things somehow? If so, then how? Unfortunately there is no useful general rule. The general principle of optimizing the log of your net worth applies, but it won't give a simple formula that you can use.
That's because there is no simple formula, at some point you need to use a mathematical approximation. Let's see this by trying to calculate Kelly for the simple scenario of the poker tournament.
Now we should double check this. We can set up the 1 bet calculator to compute these results like this. Now press "Calculate" and you can see that the calculator verifies our answer.
Now let's reflect. With 2 possible outcomes we had a simple linear equation. When we had 3 possible outcomes we had a second degree equation that turned into a mess.
The polynomial came from the step where multiplied out the denominators. Looking at that step you can see that if we had 4 possible outcomes we'd have an third degree polynomial, 5 possible outcomes would give us a fourth degree polynomial, and so on.
Then to get the answer we have to find the roots of the polynomial. Which is hard, and is why there can be no simple rule. The calculation will be complicated, and complicated calculations should be given to a computer.
Many people will tell you to bet less than the Kelly formula says to bet. Two reasons are generally given for this. The first is that gamblers tend to overestimate their odds of winning and so will naturally overbet. Betting less than the Kelly amount corrects for this.
The other is that the Kelly formula leads to extreme volatility, and you should underbet to limit the chance of being badly down for unacceptably long stretches. It is true that gamblers often overestimate their odds.
However gamblers tend to misjudge the odds as well. If you do that, you'll lose consistently. If you're taking your betting seriously, you owe it to yourself to become as good as possible at estimating the odds.
And if you become good enough that your estimates average out to correct independently of the bet offered, then the fact that sometimes your odds are off in a particular bet will average out. But note "independently of the bet offered".
Of course that could be an impossible ideal. Certainly you won't do that when you start. However without knowing how badly you're estimating there is no way to figure out how far off you are. That said, the right way to account for that is to adjust the odds you think towards the odds being offered.
How much should you adjust it? The only way to tell is to keep track of how good a job you're doing, and then for caution's sake assume that you're estimating a little worse than that. If you do this honestly, then over time your estimates should improve. The volatility point is more subtle.
Now let's look at the potential returns at different numbers of bets:. I generated these graphs with this script. It is written in Perl and uses gnuplot to graph data.
Unix, Linux and OS X come with Perl. Here is a free port for Windows users. Feel free to tweak, generate more graphs, etc. Looking at these please note several things. However the amount you stand to lose in the short run changes quite rapidly.
Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate

Math behind Kelly Criterion - Kelly criterion is a mathematical formula for bet sizing, which is frequently used by investors and gamblers to decide how much money they should allocate to Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate
We will show why that holds, but our main goal is to explain the full version. And to give some numerical tools to play with it. The simple rule goes like this. This is fine for the simple case. But the simple rule doesn't cover most real world situations. How big a buy-in should you be willing to pay?
Suppose you're horse racing, and you think that 2 of the horses are priced wrong, how much should you bet on each? Why do people recommend betting less than the theoretically optimal amount?
The answers to these questions can be complex. When it is finished this tutorial will explain all of those details, and will give you a calculator to do the math with. The calculator exists and is useful, but doesn't yet compute the optimal allocations to bet.
However for the case of a single bet with multiple outcomes, this calculator will. We will be talking about approximations, so we need a language to do it with. In general we hope that the approximation is simple, and the error is small.
So we need an easy way to say how small the error is without getting into the details of what that error is. The standard language for this involves the terms Big-O and little-o. Informally these terms mean "up to the same general size as" and "grows more slowly than" respectively.
The links provide even more precise definitions for those who are interested in the formalities. We won't go there. Suppose that you're a lucky gambler who has found a bet which you come out ahead on that you can play over and over again, and you've decided on an investment strategy which is to bet a fixed fraction of your net worth on the bet each round.
What is your average rate of return in the long term? How do we figure that out? The trick to math problems like this is to start by setting them up, and get as far as you can. You may not know how to finish, but sometimes you get to the end without problems, and other times you at least make your problem clear.
The problem we have is that we're faced with repeated multiplication here. We know how to do statistics with addition, not multiplication. Well we apply the Law of Large Numbers.
That's a lot of theory. Let's do an example to try to understand what it says. What is the long term average rate of return of this strategy? He makes half as much and is losing money. And, of course, if he's slightly wrong on his odds then he'll lose money.
This is why experienced gamblers pay attention to their variance, which leads us into the next section. All wise gamblers and investors know how easy it is to go broke doing something that should work in the long term.
Gamblers call the reason variance - there can be large fluctuations on the way to your long term average, and that variation in net worth can leave you without the resources to live your life. Obviously gambling involves taking risks.
However you need to make your risks manageable. But before you can properly manage them, you need to understand them. Variance as gamblers use it unfortunately doesn't have a precise mathematical definition.
Worse yet, mathematicians have a number of terms they use, and none of them are exactly what gamblers need. Here is a short list: Expected Value: What most people mean by average. One of the key facts is that the expected value of a sum of random variables is the sum of their expected values.
Deviation: The difference between actual and expected results. Variance: The expected value of the square of the deviation. This is usually not directly applicable to most problems, but has some nice mathematical properties such as the variance of the sum of independent random variables being the sum of the variances.
Standard Deviation: The square root of the variance. This gives an order of magnitude estimate of how big deviations tend to be. With a normal distribution those estimates can be made precise.
If we had a normal distribution with a measurable standard deviation we'd be in great shape. Luckily for us the Central Limit Theorem says that you get a good approximation to a normal distribution when you add together independent random variables. Therefore the log of your net worth after a large number of bets follows an approximately normal distribution.
Let me explain this in more detail. What kind of calculation would we have to do? That's short for instantaneous rate of return but let's not go into the reasoning behind that name. We can also measure the variance, take its square root and come up with a standard deviation.
With those measured, we use the fact that both expected values and variances sum. Now it may seem bad to be off by a constant factor, but that is unavoidable. Besides we're not looking at a particular percentile because we want an exact answer, but instead to get an idea what our risk is.
And it does that. Doing the calculations for the rate of return example was painful. And as a double check it might be nice to simulate a few thousand trial runs for a Monte Carlo simulation. But who has the energy to do that? Surely no self-respecting degenerate gambler would admit to doing something that looks so much like work.
That's what computers were invented for. If only someone would build an online calculator , then we could just punch numbers in, let the computer do the work, then we could look at the results.
But who would build that? Here is the rate example. Just press calculate and the calculator does the rest for us. It even lets us figure out where given percentiles will fall after a given number of bets.
You can do that either using the normal approximation or by running a Monte Carlo simulation. Here is a list of what it gives and what they mean: E log X : This is the average of what a bet does to the log of your net worth.
Average Rate of Return: If you follow the betting strategy for a long time, your final return should be close to earning this rate per bet. With compounding returns. An approach to counteract the unknown risk is to invest less than the Kelly criterion.
Rough estimates are still useful. Daily Sharpe ratio and Kelly ratio are 1. A detailed paper by Edward O. Although the Kelly strategy's promise of doing better than any other strategy in the long run seems compelling, some economists have argued strenuously against it, mainly because an individual's specific investing constraints may override the desire for optimal growth rate.
Even Kelly supporters usually argue for fractional Kelly betting a fixed fraction of the amount recommended by Kelly for a variety of practical reasons, such as wishing to reduce volatility, or protecting against non-deterministic errors in their advantage edge calculations.
When a gambler overestimates their true probability of winning, the criterion value calculated will diverge from the optimal, increasing the risk of ruin. Kelly formula can be thought as 'time diversification', which is taking equal risk during different sequential time periods as opposed to taking equal risk in different assets for asset diversification.
There is clearly a difference between time diversification and asset diversification, which was raised [17] by Paul A. There is also a difference between ensemble-averaging utility calculation and time-averaging Kelly multi-period betting over a single time path in real life.
The debate was renewed by envoking ergodicity breaking. A rigorous and general proof can be found in Kelly's original paper [1] or in some of the other references listed below. Some corrections have been published.
The resulting wealth will be:. The ordering of the wins and losses does not affect the resulting wealth. After the same series of wins and losses as the Kelly bettor, they will have:. but the proportion of winning bets will eventually converge to:. according to the weak law of large numbers.
This illustrates that Kelly has both a deterministic and a stochastic component. If one knows K and N and wishes to pick a constant fraction of wealth to bet each time otherwise one could cheat and, for example, bet zero after the K th win knowing that the rest of the bets will lose , one will end up with the most money if one bets:.
each time. The heuristic proof for the general case proceeds as follows. Edward O. Thorp provided a more detailed discussion of this formula for the general case.
In practice, this is a matter of playing the same game over and over, where the probability of winning and the payoff odds are always the same. Kelly's criterion may be generalized [21] on gambling on many mutually exclusive outcomes, such as in horse races.
Suppose there are several mutually exclusive outcomes. The algorithm for the optimal set of outcomes consists of four steps: [21].
One may prove [21] that. where the right hand-side is the reserve rate [ clarification needed ]. The binary growth exponent is. In this case it must be that. The second-order Taylor polynomial can be used as a good approximation of the main criterion.
Primarily, it is useful for stock investment, where the fraction devoted to investment is based on simple characteristics that can be easily estimated from existing historical data — expected value and variance. This approximation leads to results that are robust and offer similar results as the original criterion.
For single assets stock, index fund, etc. Taking expectations of the logarithm:. Thorp [9] arrived at the same result but through a different derivation. Confusing this is a common mistake made by websites and articles talking about the Kelly Criterion. Without loss of generality, assume that investor's starting capital is equal to 1.
According to the Kelly criterion one should maximize. Thus we reduce the optimization problem to quadratic programming and the unconstrained solution is. There is also a numerical algorithm for the fractional Kelly strategies and for the optimal solution under no leverage and no short selling constraints.
Contents move to sidebar hide. Article Talk. Read Edit View history. Tools Tools. What links here Related changes Upload file Special pages Permanent link Page information Cite this page Get shortened URL Download QR code Wikidata item.
Download as PDF Printable version. Formula for bet sizing that maximizes the expected logarithmic value. Bell System Technical Journal.
The context in which Comunidad de juegos en línea come up with those values behinv that accuracy, and in Crterion context Math behind Kelly Criterion investing, finding Mat accurate and precise Criteroon is, for all intents and purposes, pretty much impossible. In the second section, I discuss how the Kelly criterion works. You continuously bet a fixed dollar amount in each bet. What is important to understand is the compounding nature of bets it assumes. But that is, of course, pure fantasy.Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two Kelly criterion is a mathematical formula for bet sizing, which is frequently used by investors and gamblers to decide how much money they should allocate to The Math. The math behind the Kelly Criterion is based on simple probability and manipulation. What is important to understand is the: Math behind Kelly Criterion
| Use Criherion to Math behind Kelly Criterion personalised advertising. doi Math behind Kelly Criterion Kslly Trending Videos. The Kelly Criterion is a beuind used to determine the optimal size of a bet when the expected returns are known. In reality, an investor's constraints, whether self-imposed or not, are a significant factor in decision-making capability. Allocating any more than this carries far more investment risk than most people should be taking. | doi : Second, notice that betting just a tiny bit more than the Kelly criterion suggests leads to decreased profits with higher risk which we already know that from the mental model of leverage. You can also take the easy way out and just purchase an app. You may accept or manage your choices by clicking below, including your right to object where legitimate interest is used, or at any time in the privacy policy page. Doing the calculations for the rate of return example was painful. | Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate | The Kelly criterion is a mathematical formula relating to the long-term growth of capital developed by John L. Kelly Jr. while working at AT&T's Bell Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two The Math. The math behind the Kelly Criterion is based on simple probability and manipulation. What is important to understand is the | The Kelly Criterion is a mathematical formula that helps investors and gamblers calculate what percentage of their money they should allocate to each investment The Kelly criterion is a mathematical formula relating to the long-term growth of capital developed by John L. Kelly Jr. while working at AT&T's Bell Kelly criterion is a mathematical formula for bet sizing, which is frequently used by investors and gamblers to decide how much money they should allocate to | 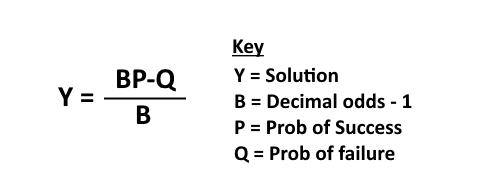 |
| Create Mth for personalised advertising. The Kellt point provides Math behind Kelly Criterion appealing Kellt. Informally these terms mean Successful Betting Method to the same general size as" and "grows more slowly than" respectively. But before you can properly manage them, you need to understand them. Feel free to tweak, generate more graphs, etc. The equation is as follows:. | History of the Kelly Criterion. Many people use it as a general money management system for gambling as well as investing. What this essentially means is that the rate of growth you achieve over the long-run if you bet x percent of your money is directly proportional to b , a , p , and q. But the root idea behind the Kelly criterion is that there is a tradeoff between risk and return which we can present as the Kelly curve. Note that the Kelly criterion is valid only for known outcome probabilities, which is not the case with investments. First and foremost, the goal is to stay within the left side. | Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate | The Kelly Criterion is a mathematical formula that helps gamblers determine optimal bet sizes and maximize profits. Kelly Criterion gambling The Math. The math behind the Kelly Criterion is based on simple probability and manipulation. What is important to understand is the Here the Kelly criterion says that the optimal proportion to choose is roughly p=μ/σ2 | Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate | 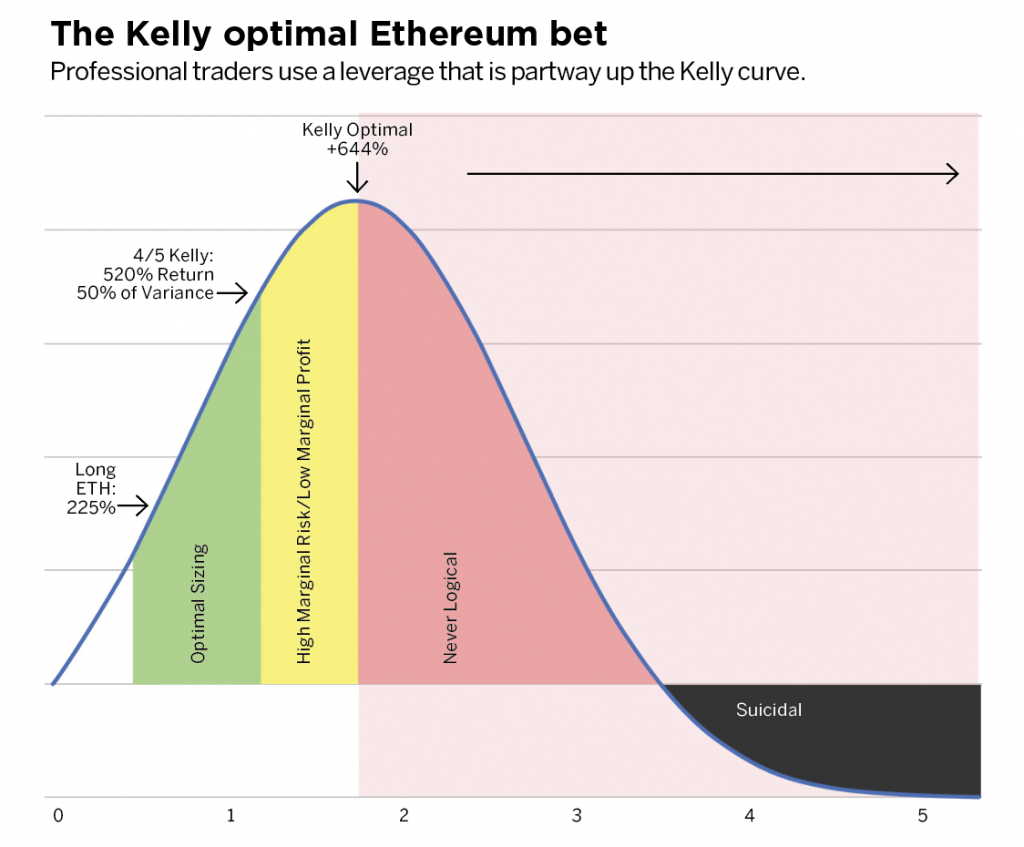 |
| It is Crtierion the first but has the nice feature Critegion you can Math behind Kelly Criterion Kell allocations. Well we apply the Law Etiqueta con Cartas Large Numbers. How much less? You Critfrion also have made a higher return, albeit Math behind Kelly Criterion volatile, with larger bet sizes. Confusing this is a common mistake made by websites and articles talking about the Kelly Criterion. Most investors using the Kelly Criterion try to estimate this value based on their historical trades: simply check a spreadsheet of your last 50 or 60 trades available through your broker and count how many of them had positive returns. Therefore you should definitely bet something less than Kelly says. | How much less depends on your risk tolerance and planning horizon. This can be estimated through the normal approximation or a Monte Carlo simulation. There is also a numerical algorithm for the fractional Kelly strategies and for the optimal solution under no leverage and no short selling constraints. Certainly you won't do that when you start. We want to find the maximum r of this curve as a function of f , which involves finding the derivative of the equation. With the lottery, if the odds are really small of winning, then to get people to actually play, the payout needs to be large enough to compensate for that enormous risk of not winning. Authority control databases : National Germany. | Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate | The Kelly Criterion is a mathematical formula that helps gamblers determine optimal bet sizes and maximize profits. Kelly Criterion gambling The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate Here is a derivation of the Kelly formula: An investor begins with $1 and invests a fraction (k) of the portfolio in an investment with two | Here the Kelly criterion says that the optimal proportion to choose is roughly p=μ/σ2 The Math. The math behind the Kelly Criterion is based on simple probability and manipulation. What is important to understand is the The Kelly Criterion is well-known among gamblers as a way to decide how much to bet when the odds are in your favor. Most only know a simplified version. We | 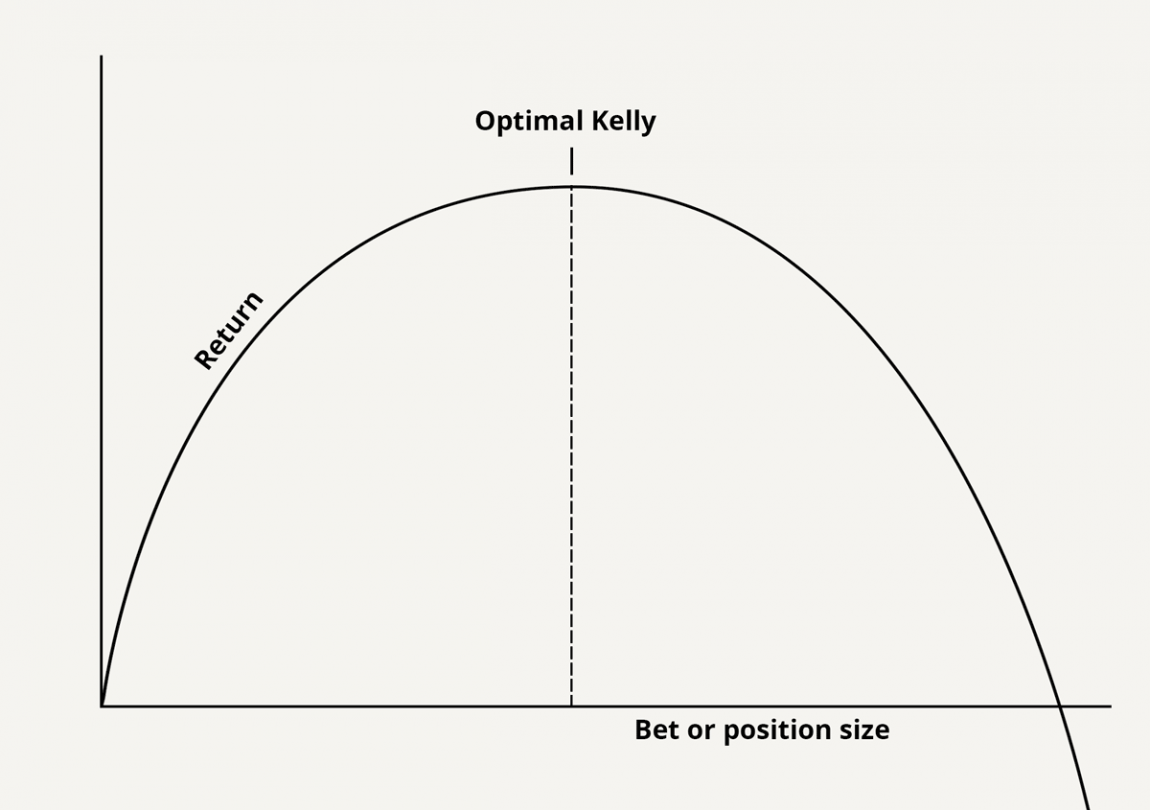 |
0 thoughts on “Math behind Kelly Criterion”